Proptest strategies the hard way
Proptest is a Rust crate for property-based testing. It provides data generators for standard types and ways how to combine and transform those to create instances of your own types. You can also use proptest-derive crate for implementing the generator for your type automatically. All this is useful, but in more complicated cases it makes sense to implement this manually. And this post shows how to do that. It is based on my experience writing generators for gryf graph library.

“Chess is an abstract strategy game” – Wikipedia. Photo by Felix Mittermeier on Unsplash
The preliminary for reading this is a basic familiarity with property-based testing in general and proptest crate in particular. Proptest book provides a very nice introduction to both. This is not a tutorial for either.
Table of contents
Strategy and ValueTree traits #
The core for generating data in proptest lies in
Strategy and
ValueTree traits.
Strategy knows how to create a ValueTree, which carries the generated value and knows how to simplify it.
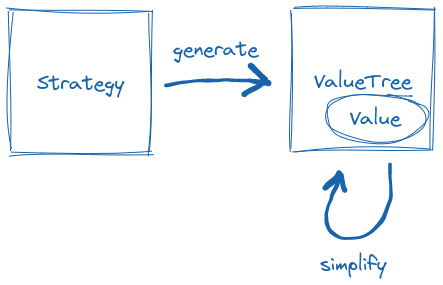
Strategy generates a value tree, which carries the generated value and knows how to simplify it.
This is an important difference from quickcheck crate,
where you can have only a single implementation of Arbitrary for a type,
which specifies how a value is generated and simplified.
In proptest, you can implement multiple different strategies for a type,
which will share the shrinking implementation defined by the value tree[1]
Technically, you can also have multiple ValueTree implementations for a type.
But I am not sure where it would be useful in practice.
Apart from special adapters like NoShrink..
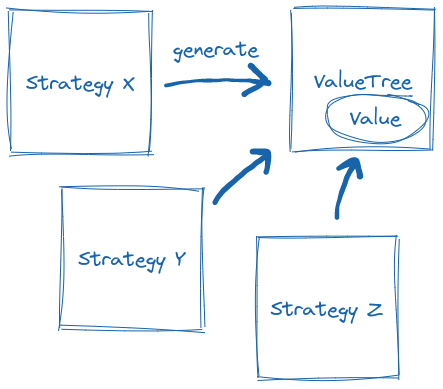
There can be multiple strategies generating the same value tree.
Let’s see the actual definition of these two traits:
pub trait Strategy: fmt::Debug {
type Tree: ValueTree<Value = Self::Value>;
type Value: fmt::Debug;
fn new_tree(&self, runner: &mut TestRunner) -> NewTree<Self>;
// Provided methods
// ...
}
pub type NewTree<S> = Result<<S as Strategy>::Tree, Reason>;
pub trait ValueTree {
type Value: fmt::Debug;
fn current(&self) -> Self::Value;
fn simplify(&mut self) -> bool;
fn complicate(&mut self) -> bool;
}Note that there is also the Arbitrary trait, but it is not fundamental for generating and shrinking the values.
It is optional.
If implemented, it represents a canonical strategy for a type and enables using any::<MyType>() (and relatives) for producing a strategy.
Shrinking as a state machine #
In the trait definition of ValueTree there are simplify and complicate methods, both taking &mut self.
This might be surprising at first – why would we want to complicate things? Aren’t they complicated enough?
The reason is that a value tree is actually some form of a state machine that is used for searching over the input space of the type.
The state is represented by the current value and some metadata, as we will see later.
The test runner then uses these two actions to converge into a value that is (potentially) simpler than the originally found but still causes the test to fail.
Thanks to complicate, the state machine can attempt to do larger steps during simplification,
and (partially) roll back if the value is not failing anymore.
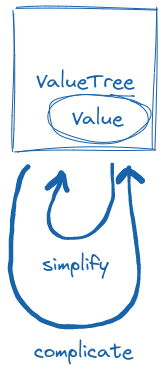
Value tree knows not only how to simplify a value, but also how to complicate it. Using these actions, the test runner tries to converge into a minimal reproducer.
From the documentation for the ValueTree trait (emphasis mine):
Conceptually, a ValueTree represents a spectrum between a “minimally complex” value and a starting, randomly-chosen value. For values such as numbers, this can be thought of as a simple binary search, and this is how the ValueTree state machine is defined.
Using binary search makes sense. You have a value that you know that it’s failing – this is the initial high. Your type (most likely) also has a trivial value (i.e., “minimally complex”, e.g. an empty string or 0) – this is the initial low. The goal is to find a value that is as minimal as possible but still failing. Binary search is an efficient way for achieving this goal (it is for example what git bisect uses for finding the commit that introduced a bug).

For types whose values have a strict total order, binary search is the most efficient way to find the minimal reproducer.
The binary search analogy is great for understanding the simplification process in proptest. However, for more complicated types (like graphs, but even vectors), the values on a “complexity scale” between failing and trivial may not lie on a straight line. Imagine a vector [1, 2, 3]. Either of the elements can be removed resulting in [2, 3], [1, 3] or [1, 2], respectively, and all these simplifications are valid options. In such situations, you could think of it more as a lattice[2]Finally I can use this term outside of the university!, as illustrated in the following picture.
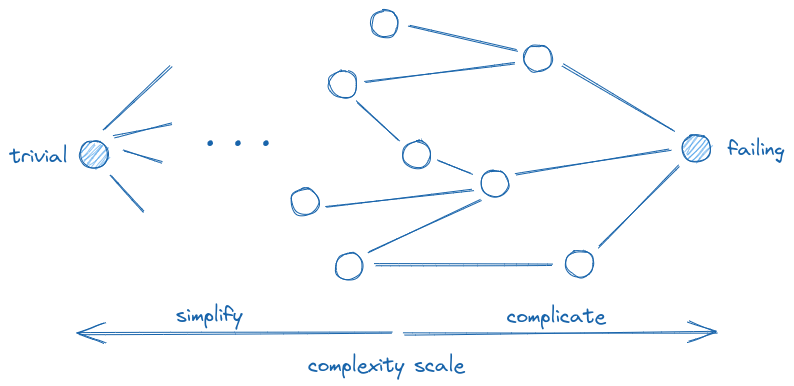
An illustration of a more complicated simplification process.
During simplification, you take one branch and test the value. If it still causes a failure, you continue going down. Once you reach a value that doesn’t fail, you take a step back and try the next branch. When you tried all branches from a value and none of them caused a failure, you got to a minimal reproducer[3]This claim is not really true in general. Possibly, there could exist a branch from one of the value’s ancestors which could lead to an even smaller reproducer but was not tried. If this is true for your type, consider making the extra effort to make the simplification traverse all possible paths so you are guaranteed to get an actually minimal reproducer..
Now I drew the illustration with values that have multiple “parents”.
This represents a situation where you can get to a value in different ways.
In a vector with at least two elements, you can get to an empty vector by removing the elements in different orders.
But in the implementation of ValueTree, you have to make sure that calling complicate will get you back to the parent on which you previously called simplify, not an arbitrary parent.
Otherwise, you could introduce cycles and your shrinking process might never terminate.
Internal representation #
The design of proptest, in particular the existence of ValueTree encapsulation of the generated value,
allows thinking about how to represent the value under the hood.
Because in more complicated cases, it may be valuable to choose a representation that is not the actual type it represents.
Why? Because we must not forget that we will eventually be asked to simplify the values of our type[4]
Unless you are the type of a programmer who writes code without bugs.,
and if our type is complex, it may not be an easy task.
So we want to generate value trees that satisfy the following goals:
- It is fast to produce the value of the target type corresponding to the value tree.
- It is reasonably easy to manipulate the value tree during the shrinking process.
These two might be in tension, so the goal is to find a good balance.

The representation must be fast to convert to the value itself as well as convenient to manipulate during the shrinking process. These two requirements might be in tension.
Let’s see some examples…
Graphs #
In gryf, the value tree is represented by (simplified)
vertices: Vec<V>andedges: Vec<(usize, usize, E)>‚removed_vertices: HashSet<usize>andremoved_edges: HashSet<usize>.
Generating the representation of a graph is filling vertices and edges vectors (the details of this are not important here).
Producing the real graph from it consists of these steps:
- Add all vertices from
vertices, but only if their indexes are not inremoved_vertices. - Add all edges from
edges, but only if their indexes are not inremoved_edgesor neither of their endpoints is inremoved_vertices.
Simplifying and complicating the graph is then done by adding and removing elements from removed_vertices or removed_edges.
This is much simpler than if we needed to manipulate a graph instance itself.
The main complication would be restoring the graph to its original form after removing a vertex,
where you would also need to restore all edges that led to that vertex.
Producing the graph and managing the removed sets is sufficiently fast.
Matrices #
The value tree for a matrix type could be represented by
elements: Vec<T>(a linear representation of the matrix, which is a common technique, having length of n_rows x n_cols),removed_rows: HashSet<usize>andremoved_cols: HashSet<usize>.
Filling the matrix is done by iterating over the elements,
calculating the row (index / n_cols) and column (index % n_cols) for the element
and adding the element to the matrix only if the row or column are not in removed_rows and removed_cols, respectively.
Although it would be somewhat straightforward to actually remove a row from the elements vector using Vec::drain,
there is no such a nice way to remove a column (which is scattered over the vector),
and adding both back during complication would not be fun either, and likely less efficient in terms of the whole process (don’t quote me on that).
Generation implementation #
This could be a one-paragraph section:
Use the rand::Rng generator
accessible via TestRunner::rng
to generate the internal representation of your choice and return it.
Nevertheless, let’s see how are generators implemented for some primitives and standard types in proptest itself.
If you are not interested in implementation details, you might want to skip to the summary of general techniques.
Floats #
The source for generating a float is here. The strategy holds the set of allowed float types (positive, normal, subnormal, infinite, …). So it is possible to customize the strategy to produce values from desired categories. From a high level, the strategy generates random bits of the float’s bit-width, which is then refined to comply with the allowed float types.
It starts with defining some helper masks (substitute $typ with f32 or f64, and see the definition of used constants if you are interested):
let sign_mask = if flags.contains(FloatTypes::NEGATIVE) {
$typ::SIGN_MASK
} else {
0
};
let sign_or = if flags.contains(FloatTypes::POSITIVE) {
0
} else {
$typ::SIGN_MASK
};
let quiet_or = ::core::$typ::NAN.to_bits() &
($typ::EXP_MASK | ($typ::EXP_MASK >> 1));
let signaling_or = (quiet_or ^ ($typ::EXP_MASK >> 1)) |
$typ::EXP_MASK;This is then followed by generating some more helper masks and flags for a particular class, selected by a weighted choice from allowed classes:
macro_rules! weight {
($case:ident, $weight:expr) => {
if flags.contains(FloatTypes::$case) {
$weight
} else {
0
}
}
}
let (class_mask, class_or, allow_edge_exp, allow_zero_mant) =
prop_oneof![
weight!(NORMAL, 20) => Just(
($typ::EXP_MASK | $typ::MANTISSA_MASK, 0,
false, true)),
weight!(SUBNORMAL, 3) => Just(
($typ::MANTISSA_MASK, 0, true, false)),
weight!(ZERO, 4) => Just(
(0, 0, true, true)),
weight!(INFINITE, 2) => Just(
(0, $typ::EXP_MASK, true, true)),
weight!(QUIET_NAN, 1) => Just(
($typ::MANTISSA_MASK >> 1, quiet_or,
true, false)),
weight!(SIGNALING_NAN, 1) => Just(
($typ::MANTISSA_MASK >> 1, signaling_or,
true, false)),
].new_tree(runner)?.current();This part of the code uses prop_oneof! macro
which produces a strategy that performs the choice.
In general, you can use other strategies as building blocks inside your strategy.
Note however that you lose the shrinker for the value unless you store the value tree itself produced by the strategy.
Then a random bit representation is generated (substitute <$typ as FloatLayout>::Bits with u32 or u64):
let mut generated_value: <$typ as FloatLayout>::Bits =
runner.rng().gen();The bits are then manipulated using the bit masks produced before:
generated_value &= sign_mask | class_mask;
generated_value |= sign_or | class_or;
let exp = generated_value & $typ::EXP_MASK;
if !allow_edge_exp && (0 == exp || $typ::EXP_MASK == exp) {
generated_value &= !$typ::EXP_MASK;
generated_value |= $typ::EXP_ZERO;
}
if !allow_zero_mant &&
0 == generated_value & $typ::MANTISSA_MASK
{
generated_value |= 1;
}Finally, the BinarySearch value tree is returned with float converted from the bits:
Ok(BinarySearch::new_with_types(
$typ::from_bits(generated_value), flags))This example shows these three techniques:
- Using other strategies as building blocks.
- Refining a random value according to the requirements specified by the strategy parameters.
- Using a different representation during generation (
u32oru64). Although this representation is converted into the target type eagerly when constructing the value tree. It’s because in this case, it makes sense to do the binary search directly on the target type.
Characters #
The core of generating a char is here. It is a function that takes
- random values generator,
- set of special characters that are considered difficult to handle in some contexts (see the list here, it’s interesting),
- preferred char ranges (generation is biased towards these to some extent), and
- allowed char ranges (the generated character must be within one of these ranges),
and returns the (base, offset) pair, where the produced character is char::from_u32(base + offset).
The base value is used for choosing a somehow more clever low bound for the shrinking process.
The generation proceeds as follows. First, there is a 50% chance that a special character is chosen (but only if it is included in allowed ranges):
if !special.is_empty() && rnd.gen() {
let s = special[rnd.gen_range(0..special.len())];
if let Some(ret) = in_range(ranges, s) {
return ret;
}
}If a special character is not chosen, then there is a 50% chance that the character is chosen from one of the preferred ranges (but again, only if it is included in allowed ranges):
if !preferred.is_empty() && rnd.gen() {
let range = preferred[rnd.gen_range(0..preferred.len())].clone();
if let Some(ch) = ::core::char::from_u32(
rnd.gen_range(*range.start() as u32..*range.end() as u32 + 1),
) {
if let Some(ret) = in_range(ranges, ch) {
return ret;
}
}
}If neither of the preferred ranges is used, the code returns a random character from the allowed ranges.
Note that not every u32 value is a valid UTF−8 character, so char::from_u32(random_u32) can fail.
In that case, the code tries to generate a new random value.
for _ in 0..65_536 {
let range = ranges[rnd.gen_range(0..ranges.len())].clone();
if let Some(ch) = ::core::char::from_u32(
rnd.gen_range(*range.start() as u32..*range.end() as u32 + 1),
) {
return (*range.start() as u32, ch as u32 - *range.start() as u32);
}
}There is also a fallback if there was no success even after a large number of attempts:
(*ranges[0].start() as u32, 0)This example shows these two techniques:
- Bias towards supposed edge cases. This arguably increases the chance of finding a failing input, but it must not be excessive, because that would artificially narrow the search space.
- Handling invalid values produced by the random generator. The strategy should not fail in such cases if it can try harder or if there is a way how to produce at least something.
Strings #
String generation in proptest is interesting in that the shape of the strings is constrained by a regular expression.
That is, the strategy represented by "[0-9]{4}-[0-9]{2}-[0-9]{2}" will only generate strings that contain 4-digit, 2-digit and 2-digit numbers separated by hyphen.
Under the hood, the strategy first parses the regular expression into an intermediate representation (Hir) using the regex-syntax crate.
Then it matches the nodes of this representation
and returns a strategy that generates characters or bytes based on the expression.
For example,
Literal('A')will returnJust('A'), whereJustis a strategy which always produces a single given value and never shrinks, orClass(Digit)[5]Digitis here used for illustration purposes only. All character classes are already converted into their correspondingcharranges in Hir. will return a strategy that picks a random digit character from givencharranges using the approach described earlier.
Often it’s a composition of nested strategies. For example,
Repetition(subexpr, kind)will return aVecstrategy where elements (vectors of bytes) are produced by the strategy corresponding tosubexpr; the size of the vector is constrained by repetitionkindand it is then flattened to a single vector of bytes, orAlternation(subexprs)will return a strategy that randomly picks one of the strategies that correspond tosubexprsand produces a value from it.
This is a nice example of a creative way how one can parametrize a strategy that should produce values under some constraints. Another example could be generating HTTP requests specified by an OpenAPI specification:
proptest! {
#[test]
fn api_request(request in openapi(include_str!("path/to/openapi.json"))) {
// ...
}
}This example shows this one technique:
- A creative, convenient way to communicate to the strategy how to produce complex values with desired constraints.
HashMaps #
Before looking at the strategy for HashMap, we have to first see the strategy for generating Vecs. Fortunately, it is quite simple:
let (start, end) = self.size.start_end_incl();
let max_size = sample_uniform_incl(runner, start, end);
let mut elements = Vec::with_capacity(max_size);
while elements.len() < max_size {
elements.push(self.element.new_tree(runner)?);
}First, it samples the target size from the range provided by the user and then it fills the vector with elements produced by the strategy for elements (also provided by the user).
The actual implementation of the strategy for HashMap is a macro exhibition (judge for yourself),
but the idea is straightforward: Generate Vec<(K, V)> and .into_iter().collect() it to HashMap<K, V>.
This example only shows what we have already seen: using other strategies as building blocks and using a different representation during the generation. But here it is even more apparent.
Summary #
Along with generation logic that is inherently specific to your case, consider also these general techniques:
- Use other strategies as building blocks.
- Refine a random value according to the requirements specified by the strategy parameters.
- Use a different representation during the generation. One for which strategies already exist or one that is easy to manipulate during generation (and potentially shrinking).
- Bias towards supposed edge cases. But don’t overdo it.
- Handle invalid values produced by the random generator. Try harder or fall back to producing at least something.
- Provide a creative, convenient way to communicate to the strategy how to produce complex values with desired constraints.
Shrinking implementation #
Shrinking is the more complicated task from the two. This is where choosing appropriate internal representation matters. But there are also standard approaches that one can use for more complex cases.
Usually, the shrinking state machine will store
- the shrink action that is going to be applied, e.g.
Shrink::DeleteElement(usize), and - some current state, e.g.
State { removed_elements: HashSet<usize> }.
For undoing a shrink action during complication, you can choose to store one of these two:
- Shrink action that was made in the previous step.
- The snapshot of the state in the previous step.
Although (1) is simpler, sometimes reverting the previous shrink action to get to the previous state is just a little too hard or even unfeasible. In those situations, using (2) to just restore the previous state is fine and worth the space.
Still remember the lattice illustration from earlier in this post? In that picture, (1) represents going back over the shrinking edge that you took in the previous step, while (2) is just teleporting to the previous state.
It is also needed to somehow indicate that the shrinking is done.
In some cases, it is implicit (e.g., the index of the element to shrink is out of bounds);
in the others, it needs to be explicit by using None with shrink: Option<Shrink>.
The simplification more or less consists of these steps:
- Apply the current shrink action.
- Store the shrink action or current state as “previous”.
- “Increment” the shrink action (e.g., delete next element or start a new phase like shrinking the elements themselves).
The simplify implementation for Vec illustrates this process well and in consumable form.
The complication is then undoing the previous shrink action or restoring the previous state.
Again, complicate for Vec as an example.
Many types have multiple “dimensions” to shrink. Usually, they are structure and elements:
Vec<T>orMatrix<T>can be reduced in size and then in remaining elements of typeT.- A graph can be reduced in structure (vertices and edges) and then in weights (on remaining vertices and edges).
- An API request can be first stripped of optional properties and then get simplified values for the remaining.
It is usually (always?) advantageous to first shrink the structure and then the elements
because after simplifying the structure there is less work on reducing the elements.
In fact, this is exactly what, for instance, the strategy for Vec does.
It is either inconvenient or impossible to achieve this behavior without implementing a custom strategy,
at least this is what this comment in nalgebra codebase suggests:
Perhaps more problematic, however, is the poor shrinking behavior the current setup leads to. Shrinking in proptest basically happens in “reverse” of the combinators, so by first generating the dimensions and then the elements, we get shrinking that first tries to completely shrink the individual elements before trying to reduce the dimension. This is clearly the opposite of what we want. I can’t find any good way around this short of writing our own custom value tree, which we should probably do at some point.
— Nalgebra proptest/mod.rs:281
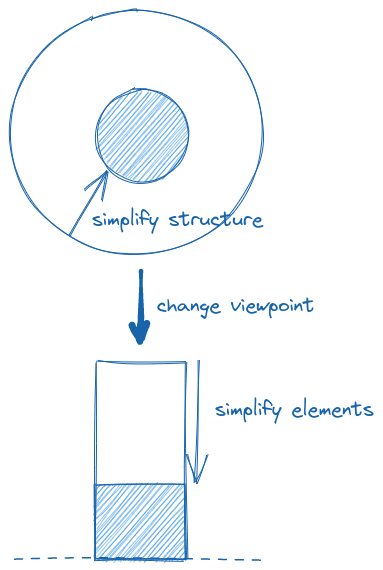
There may be preferred simplification order between the “dimensions” of the type.
Miscellaneous remarks #
Putting more effort into making the shrinking process capable will pay off when one runs into test failures. Minimizing the reproducer is an important part of property-based testing and fixing a bug with an example that is as small as possible is definitely easier than with a complicated monster.
Consider providing a specialized Debug implementation to aid diagnosis of the failure.
For example in gryf, the generated graph is wrapped in an adapter that prints the graph in DOT syntax which can be visualized by Graphviz.
For the developer who is debugging their algorithm on edge cases, this is infinitely more useful than an internal – usually incomprehensible – representation of the graph storage implementation.
I find using the builder pattern to be a very clean way for specifying optional parameters.
Since the manual implementation of a strategy gives you full control over the type,
you can add setters taking self and returning the strategy with the parameter set accordingly.
In combination with fn arb_foo() -> FooStrategy, this allows to parametrize the strategy like this:
proptest! {
#[test]
fn proptest(
// vertices edges
graph in arb_graph(any::<String>(), any::<u16>())
.max_size(100)
.connected()
.class(GraphClass::Bipartite)
) {
// ...
}
}Conclusion #
After reading this post, you hopefully have a better idea of how proptest strategies work under the hood and know some general techniques on how to implement your own manually.
I will once again repeat that the default approach for testing with proptest is
to use the standard strategies provided by the crate and compose them using
provided tools. Choosing the manual implementation should be considered
only if that brings substantial benefits in the quality of generated values, quality of shrinking
or easier maintenance if the value generation logic with all those combinators like prop_map or prop_filter went too wild.
In the end, I myself learned new things while writing this post and will likely incorporate them into the implementation in gryf at some point.
Technically, you can also have multiple
ValueTreeimplementations for a type. But I am not sure where it would be useful in practice. Apart from special adapters likeNoShrink. ↩︎Finally I can use this term outside of the university! ↩︎
This claim is not really true in general. Possibly, there could exist a branch from one of the value’s ancestors which could lead to an even smaller reproducer but was not tried. If this is true for your type, consider making the extra effort to make the simplification traverse all possible paths so you are guaranteed to get an actually minimal reproducer. ↩︎
Unless you are the type of a programmer who writes code without bugs. ↩︎
Digitis here used for illustration purposes only. All character classes are already converted into their correspondingcharranges in Hir. ↩︎