Introducing gryf: A new graph library for Rust
Gryf is a new graph data structure library for Rust aspiring to be convenient, versatile, correct and performant. This post describes what it is, what its state is, why to use it and some miscellaneous bits. Besides merely introducing it, I will also talk about details that are interesting to me and I am proud of.
This post is quite long, with loads of text (but also diagrams, plots and “tables”). Feel free to skip to only sections that you are interested in. If you just need a short introduction, examples and API reference, check out the documentation on docs.rs instead.
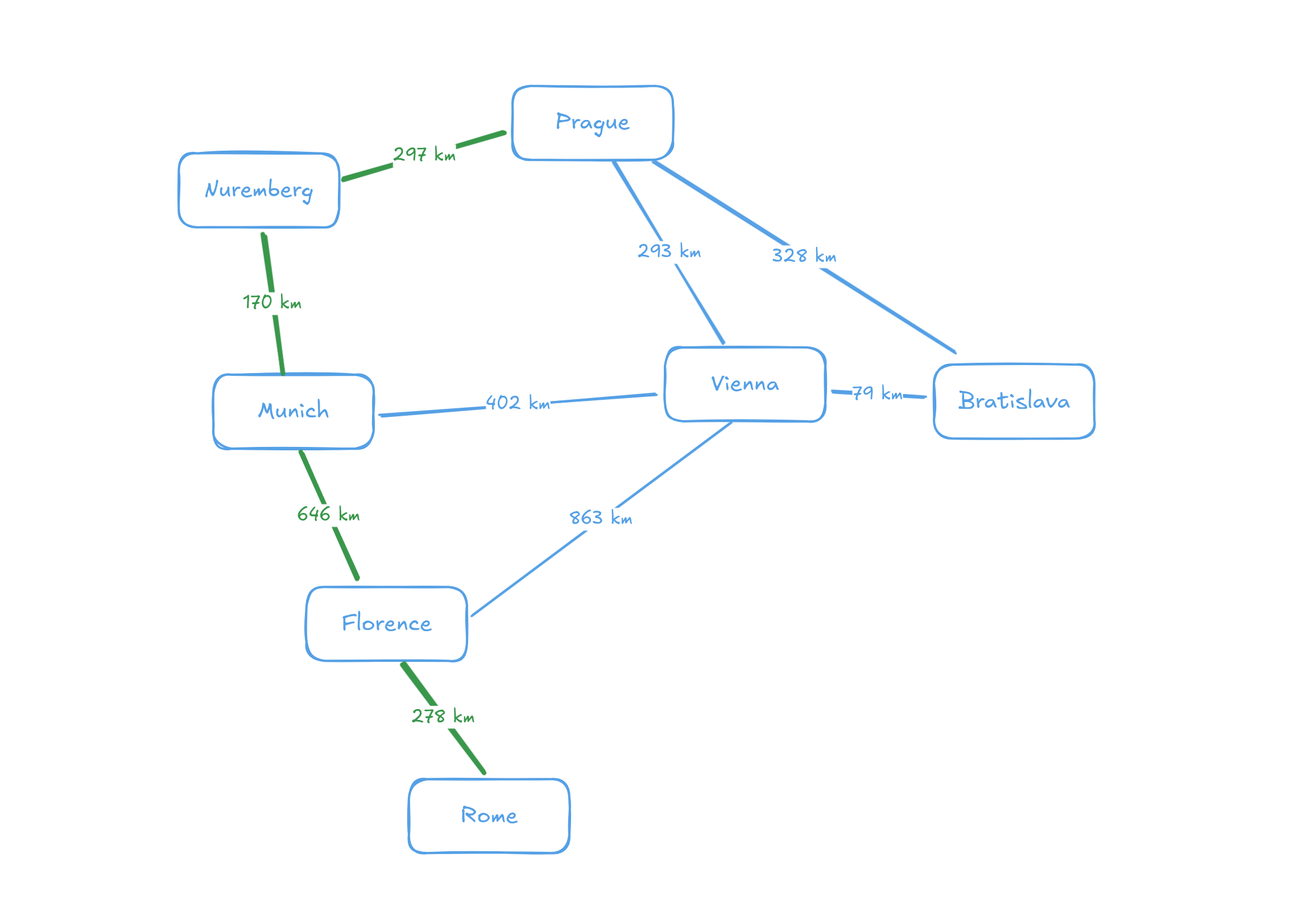
Example graph from the gryf documentation. No deep meaning really, just for the sake of having a picture in a blog post. But now you at least know how many kilometers there is on a road from Florence to Rome.
Table of contents
Example #
Before jumping into the content, let’s see an example so you get a feeling how gryf looks like. It’s nothing spectacular or unique, yet I believe there are some interesting ideas visible already in this short code snippet.
use gryf::{Graph, algo::ShortestPaths};
// Default storage is adjacency list, but that can be simply changed by
// using `Graph::new_undirected_in`.
let mut graph = Graph::new_undirected();
let prague = graph.add_vertex("Prague");
let bratislava = graph.add_vertex("Bratislava");
let vienna = graph.add_vertex("Vienna");
let munich = graph.add_vertex("Munich");
let nuremberg = graph.add_vertex("Nuremberg");
let florence = graph.add_vertex("Florence");
let rome = graph.add_vertex("Rome");
graph.extend_with_edges([
(prague, bratislava, 328u32),
(prague, nuremberg, 297),
(prague, vienna, 293),
(bratislava, vienna, 79),
(nuremberg, munich, 170),
(vienna, munich, 402),
(vienna, florence, 863),
(munich, florence, 646),
(florence, rome, 278),
]);
// As the edge weights are unsigned and there is a specific goal, Dijktra's
// algorithm is applied. For signed edges, Bellman-Ford would be used.
let shortest_paths = ShortestPaths::on(&graph).goal(prague).run(rome).unwrap();
let distance = shortest_paths[prague];
let path = shortest_paths
.reconstruct(prague)
.map(|v| graph[v])
.collect::<Vec<_>>()
.join(" - ");
println!("{distance} km from Prague through {path}");
// 1391 km from Prague through Nuremberg - Munich - Florence - RomeWhy gryf? #
The current go-to crate for graphs is petgraph, with ~12 millions downloads per month and ~800 directly dependent crates at the time of writing this post. It’s great and does its job well. If you want a battle-tested library for your serious use case, I recommend petgraph or pathfinding. Nevertheless, I thought that the user and developer experience with a graph library in Rust could be even better and I tried to materialize my ideas into a new library.
Very quickly, here is a list of features that are intriguing in my opinion:
- Referring primarily to problems (shortest paths) instead of algorithms (Dijkstra) to reduce the barrier for (non-expert) users.
- Builder pattern for algorithm parameters to provide nice API for optional values.
- Separation of graph storage (adjacency list, adjacency matrix) and semantics (unrestricted graph, path, bipartite) to turn a M × N problem into M + N problem.
- Automatic algorithm selection for the problem on given graph with certain properties.
- Support for implicit graphs.
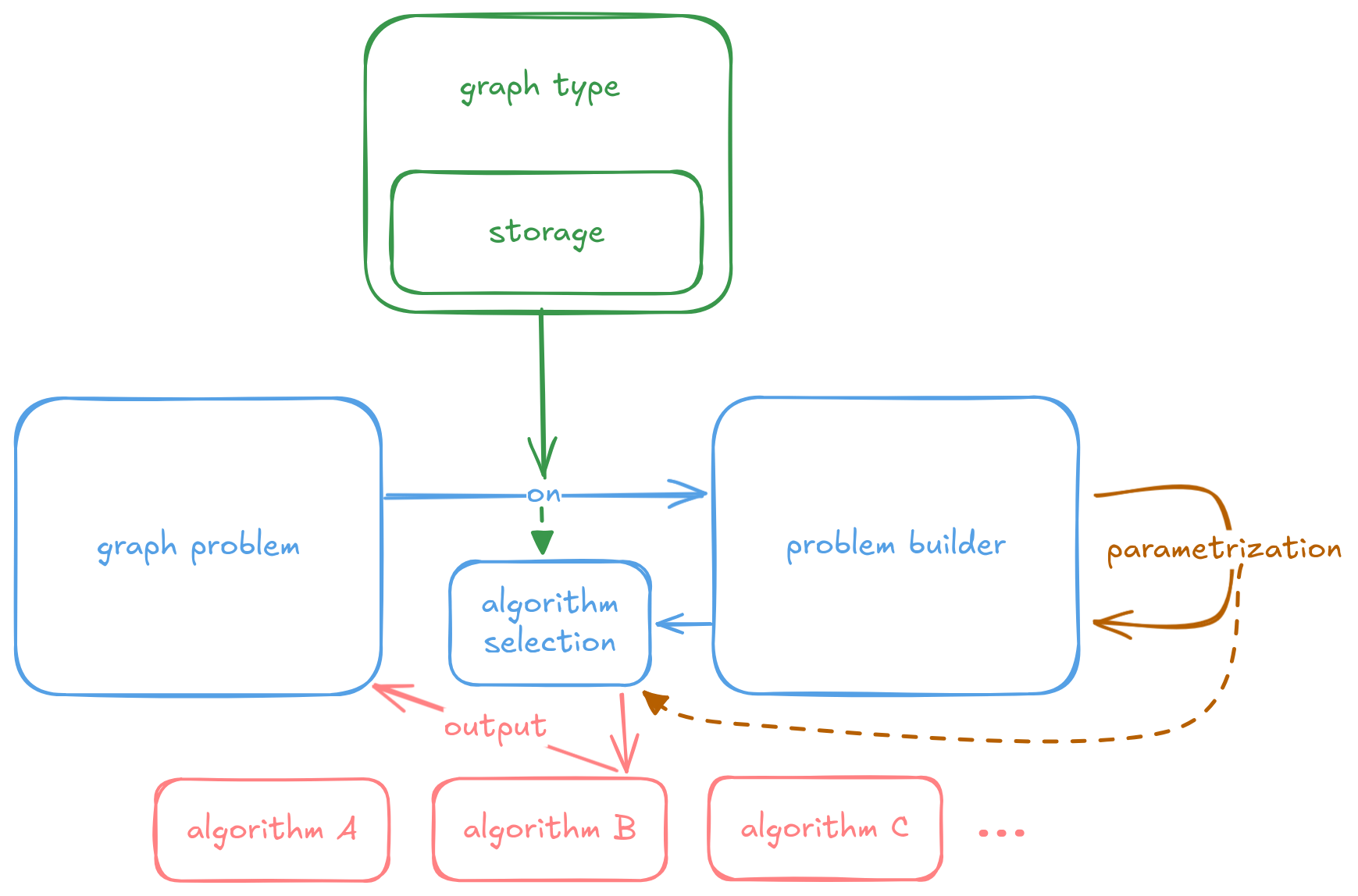
The main features of gryf illustrated in a diagram.
Now let’s look closer into each one of them. If you are not particularly excited about the details, you can skip to the Correctness section.
Problems instead of algorithms #
There are two main motivations for organizing the algorithms into the problems they solve represented by a single type. The first one is lower barrier for users, especially those that don’t have expert knowledge of graph theory. Many programmers might know the difference between Dijkstra’s and Bellman–Ford algorithms for shortest paths, as it is often in an undergraduate computer science course. But the number of people who are familiar with algorithms for more niche problems like strongly connected components, matching or dominators quickly decreases.
The assumption is that the programmers know what problem they want to solve. They could find that in a blog post, Wikipedia article, paper or told by a colleague. And that’s all they should care about in most cases – how to solve that problem should be left to the tool.
The second reason for organizing the algorithms into problems is to hide implementation details and provide additional features.
In existing graph libraries for Rust, the algorithms often return standard types like Vec or HashMap
(1, 2, 3, 4).
But that has drawbacks.
It somewhat leaks the implementation choices to the API and it cannot be changed in a backwards compatible way. But a more important consequence is that it misses a chance to provide additional functionality on the problem’s solution that a custom type could implement. Examples of these bonus features are path reconstruction for shortest paths algorithm, asking whether the found matching is perfect or not, or lazy behavior (iterators) for algorithms that allow it.
In gryf, all algorithms strictly return a dedicated new type which avoids these drawbacks.
Where it makes sense, conversion to a standard type like Vec is provided.
Builder pattern for algorithm parameters #
Algorithms can have a bunch of parameters, some of them required, some optional.
It’s not great requiring passing dummy values like None when an optional parameter is not needed,
especially when its use cases are very rare.
Moreover, adding a new optional parameter as a new function argument is a breaking change, which is also unfortunate.
The builder pattern (or you could also call it fluent API) beautifully solves these problems. That is why all algorithms in gryf follow this API structure:
let output = Problem::on(&graph)
.optional_param1(..)
.optional_param2(..)
.run(required_params);The builder types can have a handful of generic types. For example in shortest paths case, the graph, the weight type, the mapping from edge attribute to weight and the choice of algorithm are all generic types on the builder. This allows quite flexible and powerful pattern of enabling some builder methods only in specific cases.
For instance, choosing the BFS algorithm for shortest paths is allowed only when the weight mapping is of type representing “constant weight”.
Similarly, there is a different run method for each algorithm generic parameter (a closed set),
allowing different trait constraints on the graph
(e.g., Dijkstra’s algorithm doesn’t require the graph to be finite while Bellman–Ford does).
One interesting challenge was a support for floating point number weights.
Here floats not implementing the Ord trait strikes again (but I definitely not argue against that decision).
The requirement was to let the users use f32 and f64 as usual, that is,
not demanding to use a special type like from ordered-float crate.
On the other hand, having the weights being Ord is very useful in algorithm development for data structures that need it, like a priority queue.
Gryf uses a trait Weight (which is needed for other purposes anyway) with an associated type for Ordered equivalent of the type implementing the Weight trait.
For integers, this is Self (the type itself).
But for floats, it’s a new type wrapping the value and implementing the Ord trait,
specifically by using total_cmp method.
This is a compromise where users can use floats directly while in algorithms it’s just a matter of converting the weight to an Ord equivalent,
which is in all practical cases a noop.
Separation of graph storage and semantics #
There are a few standard graph representations like adjacency list, adjacency matrix and some more.
If efficiency is a goal, their implementation is not exactly trivial, with many complicated edge cases[2]I learned this the hard way by actually implementing the representations and then having fuzzing and property-based testing discovering new bugs again and again.,
so it’s essential that full-blown, performant and correct implementations of these representations are available.
Moreover, there could be use cases justifying or requiring a specialized representation for the problem.
This might be caused either by problem specifics or by the environment (embedded code[3]Support for no_std is very compelling for me and I believe that the design of gryf supports it.
However, further work and reorganization is needed to achieve this goal. or disk/network access).
On the other hand, it is beneficial to have type-level guarantees for a graph structure or properties. This includes a graph being a path, a tree, bipartite, connected, without self-loops or k-regular. Having a specific type for these classes clearly communicates the intention and makes it impossible to violate the property since only limited, specialized API is implemented on such type.
Separating the storage and the semantics allows to focus only on one task at hand during implementation and then combine available types to achieve the desired state. In a way, it turns the “M × N” problem into “M + N” problem.
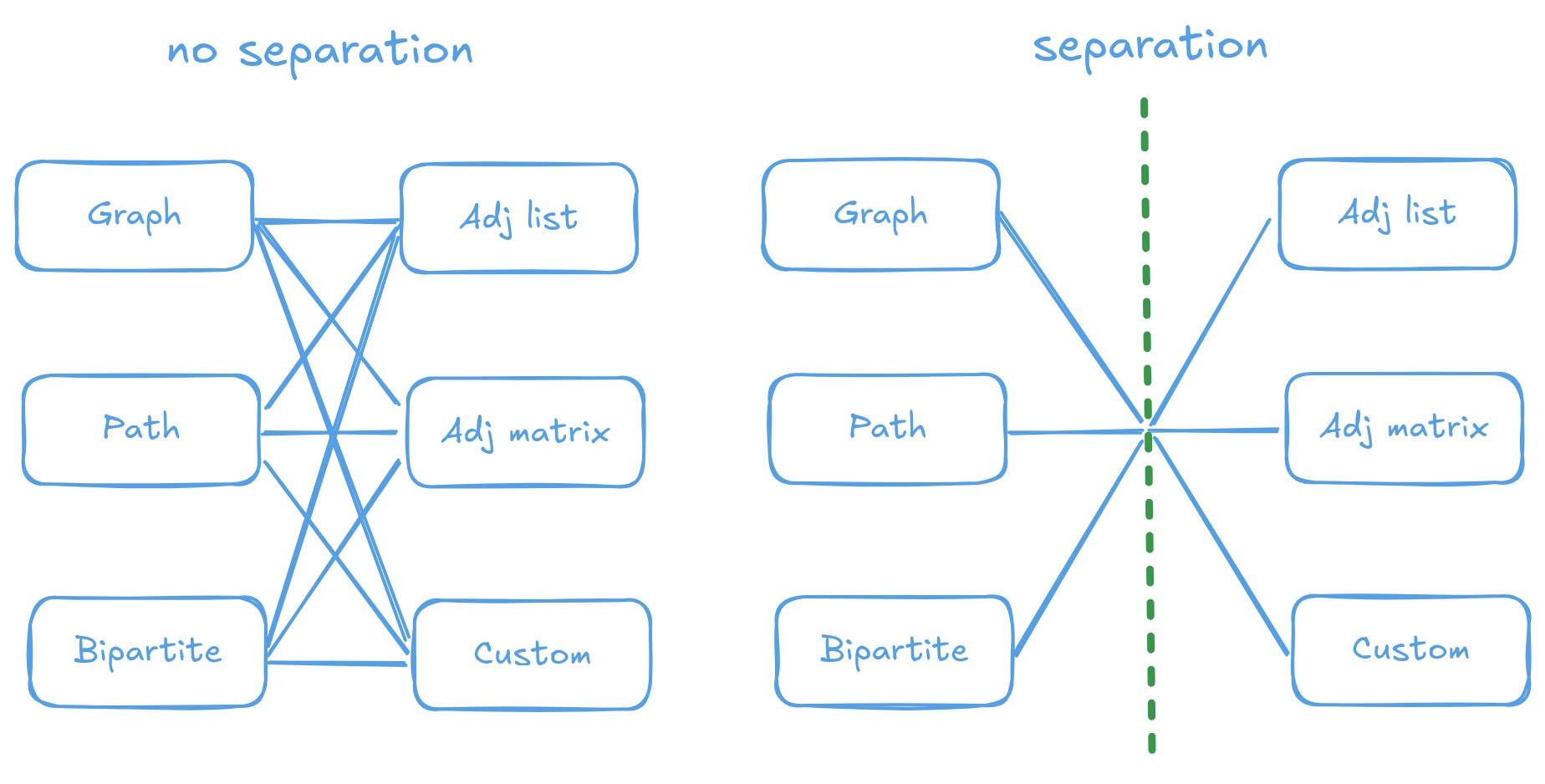
Separation of graph storage and semantics is a solution to “M × N” problem.
Automatic algorithm selection #
There is one more advantage of organizing algorithms into the problems they solve, to which I would like to dedicate its own subsection. Since the user doesn’t need to be concerned with the algorithm to be used, it can actually be the library developers that can come up with heuristics that – to the best of their knowledge, experience and benchmarks – picks the best algorithm for the task.
Such heuristic can take into account the basic properties of the graph like vertex or edge count. But perhaps more interestingly, it should also be able to check structural and other properties like graph being of certain class (bipartite, path), connected, weights being unsigned, etc. Ideally, these properties should be known at compile time to avoid runtime overhead of the checks.
Gryf tries to use trait functions without parameters[4]Associated constants could be used as well. to express guarantees known at compile time
(EdgeType::is_directed, Weight::is_unsigned, IdType::is_integer, and the entire Guarantee trait).
When compiling code for a concrete type, the compiler eliminates branches that don’t apply for that type, with zero runtime overhead.
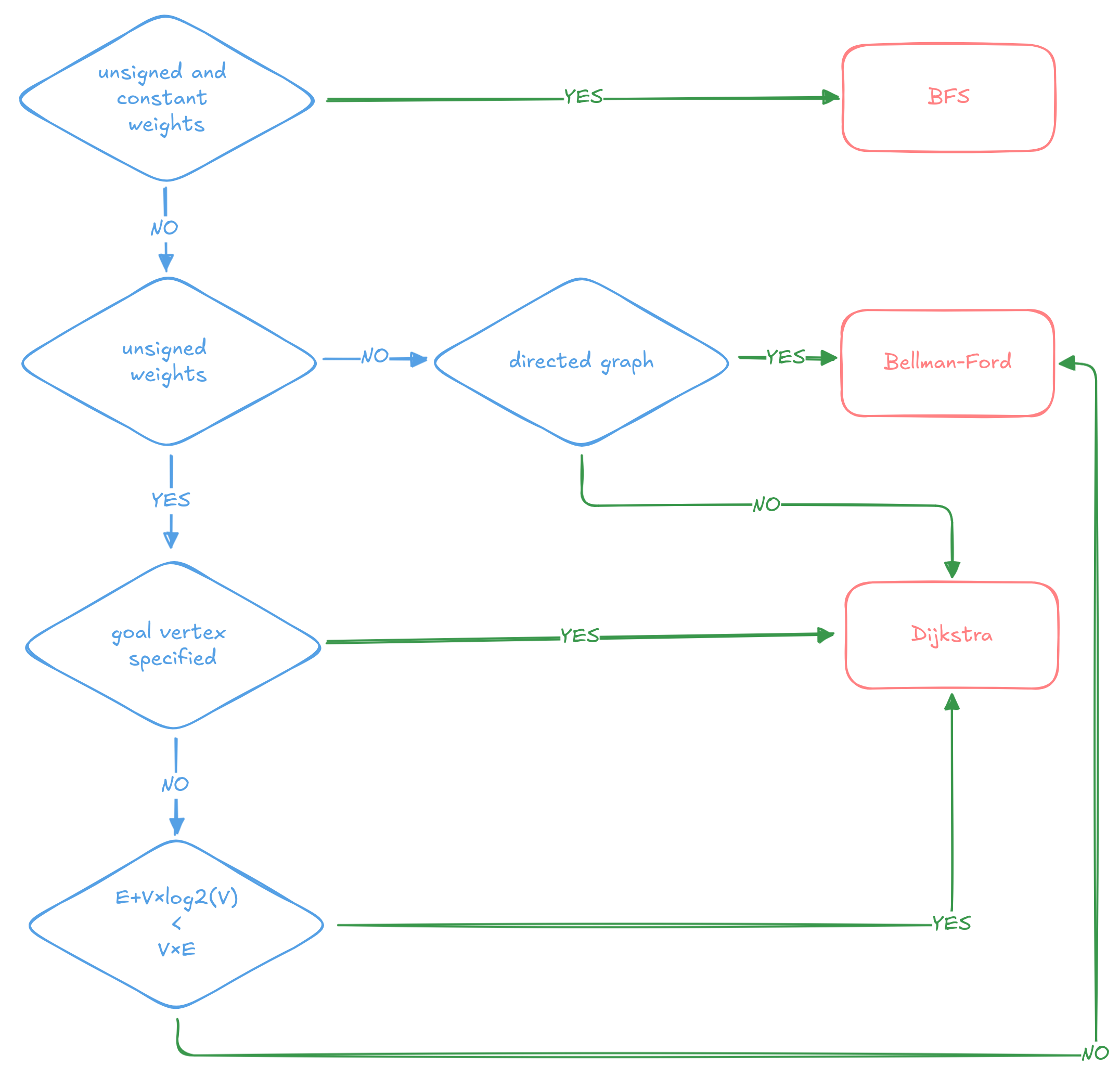
A hypothetical decision diagram for shortest paths algorithm. The E+V×log2(V) < V×E node is only for demonstration purposes, weighing in the dynamic properties of the graph and time complexities of the algorithms. In practice it would need to be more complicated.
You may also wonder about the directed graph condition. Negative weights in undirected graphs (different from negative cycles in directed graphs) makes any algorithm to error out, so we assume there are no negative weights and choose a faster method.
And here comes another challenge with floats.
Being unsigned is a valuable property of weights.
If known at compile-time, it can lead to choosing a faster algorithm that doesn’t need to deal with negative weights.
For integers, we have the family of unsigned types u8, u16, u32, u64 and usize.
But there is nothing like that for floats, which are arguably very commonly used as weights.
Gryf therefore introduces new types uf32 and uf64 which are wrappers over corresponding primitive types to which virtually all work is delegated while making sure that the value is never negative. Whether this is actually useful and worthy, I am not sure yet.
A valid concern is whether the automatic algorithm selection isn’t too magical and if it could lead to surprising behavior when choosing different algorithm for different graphs in the same program. Some sort of adaptiveness exists in various places, for example in sorting algorithm in the standard library (1, 2) or in gemm (1, 2), the matrix multiplication library used by faer. Thus, unless the selection heuristics don’t become too unpredictable, I believe that this feature is justifiable. If still in doubts, it is possible to choose a specific algorithm explicitly on the problem builder.
One nice consequence is that when a new, faster algorithm is implemented for a problem and the algorithm selection heuristic starts to prefer it, the user then just updates the version of gryf and – boom! – the program gets a nice speed-up. Performance improvements in newer versions of a library are of course common, but in this case it would still be possible even if implementations of existing algorithms were perfectly optimized. And remarkably, new and faster algorithms even for old and fundamental problems like shortest paths are still being introduced today.
Support for implicit graphs #
Implicit graphs determine the vertices or edges algorithmically based on some rules, rather than storing them explicitly in memory. I didn’t study this area that much and I haven’t found a compelling practical example other than game puzzles (Rubik’s cube, chess moves) or mathematics (Collatz problem).
But that doesn’t mean there is none. At the very least, loading parts of the graph from disk or network because the whole graph wouldn’t fit into memory might be considered as an example of implicit graph and I can definitely see a real-world use case.
There are two main elements that help this goal:
- Allowing custom types for vertex and edge IDs. That is, an ID doesn’t need to be an integer, but can be for instance a tuple of integers, or a name, or any other representation that can be used to interpret the vertex or edge.
- Traits that don’t assume finiteness of the graph
and allow returning either borrowed values (explicit graphs, standard case) or owned values (implicit graph, constructed on demand).
This is achieved by an enum that is very similar to
Cow.
Correctness #
Now I hear you asking: “Ok, that’s all nice, but isn’t it buggy?”
Correctness is very important for me, because graph is a complicated data structure that is supposed to be used as a reliable building block in the applications. Due to the complexity of implementation, unit tests are definitely not enough (but are still extensively used). That is why gryf uses fuzzing and property-based testing.
Fuzzing is a technique where pseudo-random bytes are generated and used as source data for generating higher-level types, which are then passed to the testing code. Fuzzers then, in a clever way, try to find a byte sequence that produces input that causes a crash. In gryf, fuzzing is used to generate sequences of graph operations (add vertex/edge, remove vertex/edge) that are applied on the graph storages. After that, the following properties are checked:
- Consistency of the values returned by a storage methods like all iterators produce the number of elements equal to claimed vertex/edge count, relationships between in, out and total degree, handshaking lemma, and similar. There is definitely room for more checks, but these basic properties as well as the fact that the storage doesn’t panic while applying the operations are already very valuable.
- Potential isomorphism between all pairs of storages. By “potential isomorphism” I mainly mean comparing degree sequences which is a simple and fast, yet expressive graph invariant. But it by no means guarantees real isomorphism. The idea behind is that it is unlikely that three fundamentally different implementations would be buggy in the same way.
Property-based testing is similar to fuzzing, but generates the input types directly using certain strategies and supports powerful input minimization when a failing case is found. Generated inputs are again passed into the testing code and problem-specific properties are tested. In gryf, property-based testing is mainly used for algorithms. Random graphs are generated with certain properties, the algorithm is executed and then the properties of the output are checked. Examples include
- Shortest paths and distances are calculated for all vertices if the graph is connected.
- Sequence of vertices is actually topologically sorted.
- Outputs from different algorithms have the same values (where should be).
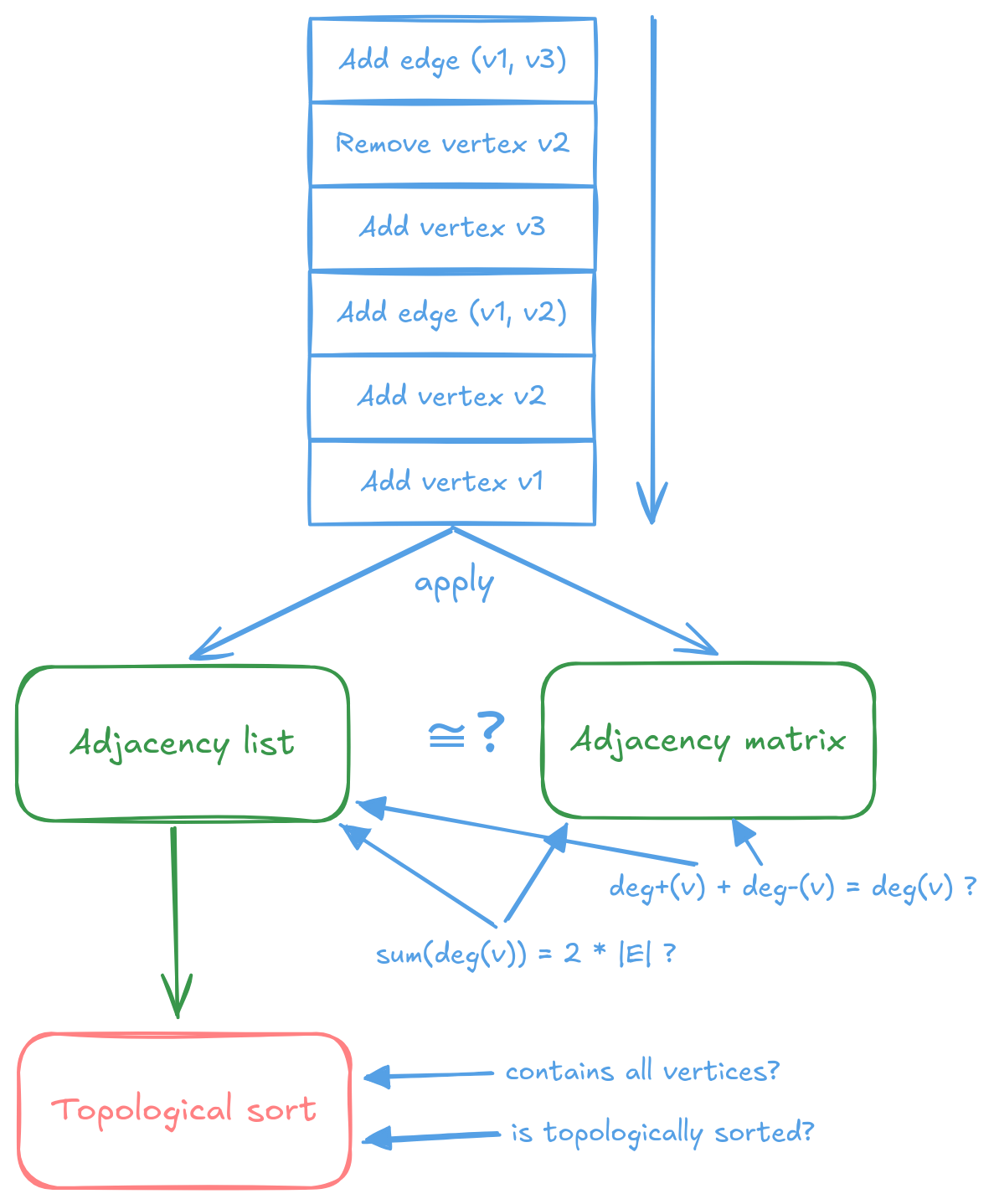
A simplified illustration of fuzzing and property-based testing used in gryf.
These two techniques did discover many bugs. The tests now run without finding any new ones[5]For fuzzing, I let them run for lower tens of minutes. While I am sure they could be running even longer, I consider it enough in the current phase of gryf’s life.. Even though they are not perfect, I am therefore fairly confident in the code correctness.
These testing techniques are used continuously on the project. Property-based tests are executed on every pull request and merge to main. Fuzzing runs at the end of every week for several minutes.
Performance #
Yet again I hear you asking: “That sounds fine, but is it fast?”
Blazi… Well, I designed and implemented gryf with performance in mind, but it was not my primary focus so far. That is why it came as a pleasant surprise to me when preliminary benchmarks showed that it’s comparable to petgraph and in some cases even better. I hope it’s not a flaw in the implementation, but given what is described in the Correctness section, I am confident in core operations working properly. If you find an issue in my code, I would appreciate a bug report so that I can correct it.
This is how the benchmarks are set up:
- For each case, results are measured for different vertex counts.
- For each vertex count, different “edge density” (probability p of an edge (u, v) being generated) is used.
- The edge generation is based on this paper.
- Vertex attributes are
u32and edge attributes aref32. This only affects the memory used. - For every benchmark, the random generator is seeded with the same seed. Thus all graphs with certain vertex count and edge density should be identical. It would be better to run the tests on different graphs, but I tried a few different random seeds with similar results. And I promise there was no random seed tuning.
First benchmark I did was “basic operations” like vertex and edge addition and removal. The process is as follows:
- Add N vertices.
- Add random edges with given edge density relative to N.
- Remove 1/4 × N random vertices.
- Remove random edges with given edge density relative to 1/4 × N.
- Add random edges with given edge density relative to 3/4 × N.
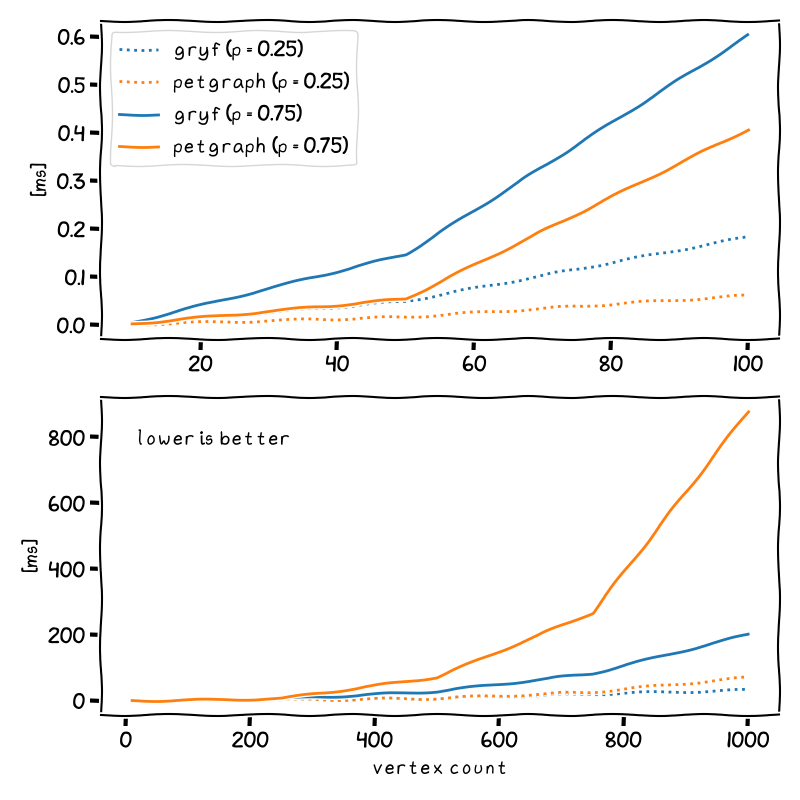
Results for the “basic operations” benchmark, comparing gryf and petgraph on small graphs (top) and larger graphs (bottom). Parameter p represents the edge density in the graph. The benchmarks setup can be found here, although different sizes and densities were used for the purposes of the plot.
It turns out that on smaller, sparse graphs, petgraph is faster than gryf. But interestingly, on larger, dense graphs, it is actually gryf who does better. This trend continues with vertex count increasing. For instance, I tried to bench N = 5000, p = 0.5 graph and results are significant with 12 seconds for gryf and 3 minutes for petgraph.
The rest of the benchmarks test the graph algorithms that gryf implements: shortest paths (Dijkstra and Bellman–Ford) and topological sort. First a graph is created with the same rules as in steps (1) and (2) above. The graph creation is not included in the time measurement. Then the algorithm is ran on the graph. The pattern with petgraph being better on smaller graphs while gryf being better on larger graphs shows up again in these cases.
Below is a full output of all benchmarks if you are interested. I also asked a friend to run the same benchmark on his Framework and Mac computers and the results were the same relatively speaking.
Full benchmark output
- Intel® Core™ i5–8265U CPU @ 1.60GHz
- 24 GiB RAM
- Arch Linux 6.9.10-arch1–1
- rustc 1.81.0-nightly (a70b2ae57 2024–06–09)
- divan v0.1.14
- Benchmarks source
╰─ benchmark
╰─ vertex count
╰─ edge densitybasic_ops fastest │ median
├─ gryf_adj_list_add_remove │
│ ├─ Directed │
│ │ ├─ 100 │
│ │ │ ├─ 0.05 72.27 µs │ 76.66 µs
│ │ │ ├─ 0.5 378.2 µs │ 433.6 µs
│ │ │ ╰─ 0.95 818.6 µs │ 924.9 µs
│ │ ╰─ 1000 │
│ │ ├─ 0.05 4.877 ms │ 5.158 ms
│ │ ├─ 0.5 105.8 ms │ 117.1 ms
│ │ ╰─ 0.95 343.2 ms │ 381.4 ms
│ ╰─ Undirected │
│ ├─ 100 │
│ │ ├─ 0.05 34.48 µs │ 35.76 µs
│ │ ├─ 0.5 384.6 µs │ 407.1 µs
│ │ ╰─ 0.95 812.2 µs │ 848.3 µs
│ ╰─ 1000 │
│ ├─ 0.05 4.178 ms │ 4.405 ms
│ ├─ 0.5 124.4 ms │ 132.9 ms
│ ╰─ 0.95 391.4 ms │ 412 ms
╰─ petgraph_graph_add_remove │
├─ Directed │
│ ├─ 100 │
│ │ ├─ 0.05 15.61 µs │ 22.95 µs
│ │ ├─ 0.5 230 µs │ 238.7 µs
│ │ ╰─ 0.95 585.7 µs │ 595 µs
│ ╰─ 1000 │
│ ├─ 0.05 2.801 ms │ 2.917 ms
│ ├─ 0.5 248.5 ms │ 313.9 ms
│ ╰─ 0.95 1.254 s │ 1.317 s
╰─ Undirected │
├─ 100 │
│ ├─ 0.05 13.56 µs │ 13.71 µs
│ ├─ 0.5 210.7 µs │ 220.1 µs
│ ╰─ 0.95 556.3 µs │ 587.1 µs
╰─ 1000 │
├─ 0.05 2.726 ms │ 2.993 ms
├─ 0.5 222.1 ms │ 243 ms
╰─ 0.95 1.051 s │ 1.113 sshortest_paths fastest │ median
├─ gryf_bellman_ford_random │
│ ├─ 100 │
│ │ ├─ 0.25 5.075 µs │ 5.229 µs
│ │ ╰─ 0.75 14.62 µs │ 15.58 µs
│ ├─ 1000 │
│ │ ├─ 0.25 515.4 µs │ 546.4 µs
│ │ ╰─ 0.75 1.584 ms │ 1.657 ms
│ ╰─ 10000 │
│ ├─ 0.25 58.05 ms │ 60 ms
│ ╰─ 0.75 179.9 ms │ 187 ms
├─ gryf_dikstra_random │
│ ├─ 100 │
│ │ ├─ 0.25 137.7 ns │ 142.7 ns
│ │ ╰─ 0.75 117.9 ns │ 120.9 ns
│ ├─ 1000 │
│ │ ├─ 0.25 106.3 ns │ 109.3 ns
│ │ ╰─ 0.75 93.85 ns │ 96.73 ns
│ ╰─ 10000 │
│ ├─ 0.25 103.7 ns │ 106.7 ns
│ ╰─ 0.75 107.7 ns │ 110.7 ns
├─ petgraph_bellman_ford_random │
│ ├─ 100 │
│ │ ├─ 0.25 5.594 µs │ 5.769 µs
│ │ ╰─ 0.75 21.86 µs │ 22.67 µs
│ ├─ 1000 │
│ │ ├─ 0.25 585.2 µs │ 617.1 µs
│ │ ╰─ 0.75 2.437 ms │ 2.553 ms
│ ╰─ 10000 │
│ ├─ 0.25 79.15 ms │ 81.87 ms
│ ╰─ 0.75 223.8 ms │ 226.9 ms
╰─ petgraph_dijkstra_random │
├─ 100 │
│ ├─ 0.25 136.7 ns │ 142.7 ns
│ ╰─ 0.75 121.8 ns │ 125.3 ns
├─ 1000 │
│ ├─ 0.25 128.2 ns │ 132.7 ns
│ ╰─ 0.75 122.7 ns │ 137.7 ns
╰─ 10000 │
├─ 0.25 131.7 ns │ 138.7 ns
╰─ 0.75 137.7 ns │ 142.7 nstoposort fastest │ median
├─ gryf_dfs_random │
│ ├─ 100 │
│ │ ├─ 0.05 13.99 µs │ 14.2 µs
│ │ ├─ 0.5 72.23 µs │ 78.33 µs
│ │ ╰─ 0.95 103.8 µs │ 107.9 µs
│ ╰─ 1000 │
│ ├─ 0.05 595.6 µs │ 639.9 µs
│ ├─ 0.5 4.869 ms │ 5.422 ms
│ ╰─ 0.95 10.95 ms │ 11.16 ms
├─ gryf_kahn_random │
│ ├─ 100 │
│ │ ├─ 0.05 4.138 µs │ 4.396 µs
│ │ ├─ 0.5 19.66 µs │ 20.84 µs
│ │ ╰─ 0.95 33.21 µs │ 35.21 µs
│ ╰─ 1000 │
│ ├─ 0.05 215.2 µs │ 234.6 µs
│ ├─ 0.5 1.871 ms │ 2.004 ms
│ ╰─ 0.95 3.546 ms │ 3.679 ms
╰─ petgraph_dfs_random │
├─ 100 │
│ ├─ 0.05 2.699 µs │ 2.753 µs
│ ├─ 0.5 15.76 µs │ 15.88 µs
│ ╰─ 0.95 27.25 µs │ 27.4 µs
╰─ 1000 │
├─ 0.05 210.7 µs │ 222.5 µs
├─ 0.5 2.584 ms │ 2.797 ms
╰─ 0.95 7.543 ms │ 12.28 msI don’t think that anyone should draw some hard conclusions from these experiments. The benchmarks were made without too much thought, just to see how gryf is roughly doing. Once I turn my focus to performance, I will make sure to create a more representative benchmark with better analysis. Only after then it will make sense to claim anything else than “it’s promising”.
Algorithms #
There are not many algorithms in gryf at this moment. The main focus was on getting the fundamentals right (and still it’s not fully there) rather than on adding algorithm after algorithm. This is where you can contribute the most. If you would like to try gryf, lack an algorithm and you are up to the challenge of implementing it, don’t hesitate!
In the first version of gryf, there are these two problems/algorithms available:
- Single source shortest paths (Dijkstra, Bellman–Ford, BFS).
- Topological sorting (Kahn, DFS).
- Graph connectivity (DFS).
- Cycle detection (DFS) and collection (BFS).
Sometimes an API design decision of a problem that must be supported by all (or most) algorithm implementations requires an “innovative” solution. For example, textbook Bellman–Ford only considers directed graphs but in gryf it should support undirected graphs as much as feasible. Or a post-order DFS on transposed graph is used for topological sorting to achieve maximum laziness.
Conclusion #
Phew, that was long! That you are still here, even if you skipped some parts, indicates that you are interested in gryf ❤. In that case I encourage you to try it!
I am very curious to hear the feedback and insights from you once you do that. Did you encounter any hiccups? Something missing? Confusing compiler error? Surprising behavior? An unnecessarily complicated concept? For anything that you think could be better please file an issue on GitHub.
One opportunity to find bugs in gryf is to replace petgraph (or any other graph library) with it and see if your project’s tests fail after that. My plan is to do exactly that on most downloaded reverse dependencies of petgraph. Not only for running tests, but also to identify all inconveniences and missing pieces during the migration. Feel free to ping me if I can help with it in your project.
Keep in mind that gryf is very much immature. I keep finding rough edges that need to be refined. There are missing core features (e.g., mutable iteration). I have no doubts there are bugs to be discovered.
One point I want to address is why to create a new graph library in Rust. Although the situation is not as bad as for bloom filters, it’s not uncommon that someone comes with a new crate for graphs which gets later abandoned[6]From 7 crates I found, 2 are active, 1 is not really active but I wouldn’t call it abandoned and 4 are not active, from which 3 got their last update in 2021 – what a year of Rust graph libraries it must have been..
And that’s fine, don’t get me wrong. But what makes gryf an exception that will not meet the same end? I am convinced that it is competitive with petgraph in terms of user experience and performance and, on top of that, comes with some new ideas that, in my opinion, makes it appealing. It’s also not a single weekend project I threw into the world – I have spent a lot of time and effort on it.
Developing a new library from scratch allows wild experimentation, and whoa, some of the changes were quite intense and substantial. This wouldn’t be possible to do in an existing crate which has (many) real users. But if the features of gryf catch attention of users and petgraph will be willing to adopt them, then I will be in favor of focusing on petgraph to avoid unnecessary competition.
I hope that you will have great time with gryf if you use it and it will help you to get your project done!
Acknowledgements #
I would also like to dedicate a part of this post to thank some people.
First and foremost, everyone who contributed to the design of petgraph, which was (I assume) mainly bluss as the original author of the library. And also to all contributors and maintainers who help to keep this crate being useful. Petgraph was the main inspiration on many design and implementation aspects, as anyone likely realizes. When I contributed the matching algorithm, some of my choices there influenced how I did things in gryf.
Then to maminrayej, the author of prepona library, in which the idea of separating graph and its storage was introduced to me, and their announcement on Reddit, where I learned about it. This clever design choice and some of my ideas sparked from a reaction to it inspired me and were actually the reason why I decided to start this whole journey.
Only tangentially related, but to everyone who helped to make generic associated types (GATs) stable in Rust, as they play an important role in the design of gryf.
I remember the excitement when I started[7]Back in spring of 2021. Had some long breaks during that period, not going to pretend otherwise. to work on gryf and added these two lines to lib.rs
#![allow(incomplete_features)]
#![feature(generic_associated_types)]and the same if not stronger excitement after some 20 months when I could remove the second line and make gryf available for stable Rust. I definitely needed to fix my code occasionally after a nightly version update and I might even have encountered an internal compiler error[8]Sadly, I don’t have a reference of it, so it may be just the skill of hallucination learned by me from today’s LLMs.. But it was a great time.
You are awesome!
But I have no doubts that I must have felt very clever when I saw the chapter about Fluent API / builder pattern in the talk describing exactly my case. ↩︎
I learned this the hard way by actually implementing the representations and then having fuzzing and property-based testing discovering new bugs again and again. ↩︎
Support for
no_stdis very compelling for me and I believe that the design of gryf supports it. However, further work and reorganization is needed to achieve this goal. ↩︎Associated constants could be used as well. ↩︎
For fuzzing, I let them run for lower tens of minutes. While I am sure they could be running even longer, I consider it enough in the current phase of gryf’s life. ↩︎
From 7 crates I found, 2 are active, 1 is not really active but I wouldn’t call it abandoned and 4 are not active, from which 3 got their last update in 2021 – what a year of Rust graph libraries it must have been. ↩︎
Back in spring of 2021. Had some long breaks during that period, not going to pretend otherwise. ↩︎
Sadly, I don’t have a reference of it, so it may be just the skill of hallucination learned by me from today’s LLMs. ↩︎